行相等的最少多米诺旋转

发表于

算法：贪心算法

贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法。

贪婪算法所得到的结果往往不是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果。

  • 贪婪算法并没有固定的算法解决框架，算法的关键是贪婪策略的选择，根据不同的问题选择不同的策略。
  • 必须注意的是策略的选择必须具备无后效性，即某个状态的选择不会影响到之前的状态，只与当前状态有关，所以对采用的贪婪的策略一定要仔细分析其是否满足无后效性。

比如前边介绍的最短路径问题(广度优先、狄克斯特拉)都属于贪婪算法，只是在其问题策略的选择上，刚好可以得到最优解。

基本思路:

  1. 建立数学模型来描述问题;
  2. 把求解的问题分成若干个子问题;
  3. 对每一子问题求解，得到子问题的局部最优解;
  4. 把子问题对应的局部最优解合成原来整个问题的一个近似最优解;

题目：行相等的最少多米诺旋转

url：https://leetcode-cn.com/problems/minimum-domino-rotations-for-equal-row/

1
2
3
4
5
6
7
在一排多米诺骨牌中，A[i] 和 B[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。（一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。）

我们可以旋转第 i 张多米诺，使得 A[i] 和 B[i] 的值交换。

返回能使 A 中所有值或者 B 中所有值都相同的最小旋转次数。

如果无法做到，返回 -1.

示例1：

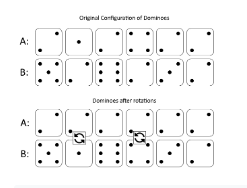
输入：A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
输出：2
解释：
图一表示：在我们旋转之前， A 和 B 给出的多米诺牌。
如果我们旋转第二个和第四个多米诺骨牌，我们可以使上面一行中的每个值都等于 2，如图二所示。

示例 2：
输入：A = [3,5,1,2,3], B = [3,6,3,3,4]
输出：-1
解释：
在这种情况下，不可能旋转多米诺牌使一行的值相等。

提示：
1 <= A[i], B[i] <= 6
2 <= A.length == B.length <= 20000

分析

分别统计A数组和B数组中每种牌出现的次数；

如果 ”A中出现的次数 x + B中出现的次数 y“ >= A数组的长度，则算是一种解；

找出所有的解，并返回 最小的 x 或者最小的 y；

如果没有满足条件的解则返回 -1；

上述求出的解是伪最优解，还需要逐个确认每个解是不是真最优解

Java解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
	public int minDominoRotations(int[] A, int[] B) {
		TreeMap<Integer,Integer> mapA = new TreeMap<Integer,Integer>();
		TreeMap<Integer,Integer> mapB = new TreeMap<Integer,Integer>();
		for(int i=0; i<A.length; ++i) {
			mapA.put(A[i], mapA.getOrDefault(A[i], 0)+1);
			mapB.put(B[i], mapB.getOrDefault(B[i], 0)+1);
		}
		int resA = minDominoRotations(A, B, mapA, mapB);
		int resB = minDominoRotations(B, A, mapB, mapA);
		if (-1 != resA && -1 != resB) {
			return Math.min(resA, resB);
		} else {
			return Math.max(resA, resB);
		}
	}

	public int minDominoRotations(int[] A, int[] B, TreeMap<Integer,Integer> mapA, 
                                  TreeMap<Integer,Integer> mapB) {
		int len = A.length, res=-1;
		TreeMap<Integer,Integer> pseudoPptimalSolution = new TreeMap<>();
		for(Map.Entry<Integer,Integer> entry : mapA.entrySet()) {
			int x = entry.getValue(), y = mapB.getOrDefault(entry.getKey(),0);
			if(x + y >= len) {
				pseudoPptimalSolution.put(entry.getKey(), len-x);
			}
		}
		for(Map.Entry<Integer,Integer> entry : pseudoPptimalSolution.entrySet()) {
			int count = 0;
			for (int i=0; i<len; ++i) {
				if (A[i] != entry.getKey() && B[i] == entry.getKey()) {
					count++;
				}
			}
			if (count == entry.getValue()) {
				res = (-1==res) ? count : Math.min(count, res);
			}
		}
		return res;
	}
}