Unique Binary Search Trees ii

发表于

算法：二叉搜索树

url：https://leetcode-cn.com/problems/unique-binary-search-trees-ii/

​

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。
示例:

输入: 3
输出:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

分析

首先来计数需要构建的二叉树数量。可能的二叉搜素数数量是一个 卡特兰数。

我们跟随上文的逻辑，只是这次是构建具体的树，而不是计数。

算法

我们从序列 1 ..n 中取出数字 i，作为当前树的树根。于是，剩余 i - 1 个元素可用于左子树，n - i 个元素用于右子树。
如 前文所述，这样会产生 G(i - 1) 种左子树 和 G(n - i) 种右子树，其中 G 是卡特兰数。

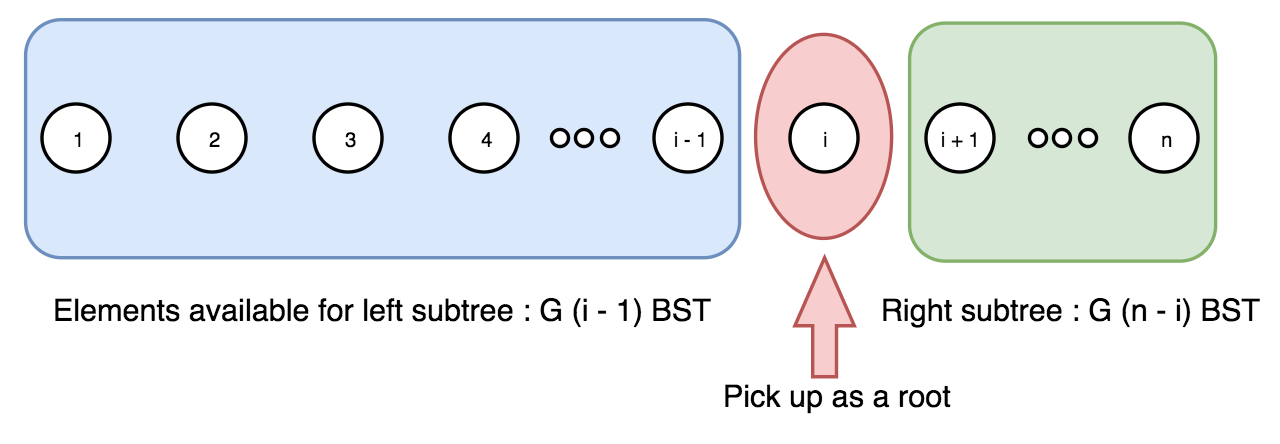
image.png

现在，我们对序列 1 … i - 1 重复上述过程，以构建所有的左子树；然后对 i + 1 … n 重复，以构建所有的右子树。

这样，我们就有了树根 i 和可能的左子树、右子树的列表。

最后一步，对两个列表循环，将左子树和右子树连接在根上。

​

Java解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n <= 0) {
            return new LinkedList<TreeNode>();
        }
        return listTrees(1, n);        
    }
    
    public LinkedList<TreeNode> listTrees(int start, int end) {
        LinkedList<TreeNode> rootList = new LinkedList<TreeNode>();
        if(start > end) {
            rootList.add(null);
            return rootList;
        }
        for(int i=start; i<=end; ++i) {
            LinkedList<TreeNode> leftList = listTrees(start, i-1); 
            LinkedList<TreeNode> rightList = listTrees(i+1, end);
            for(TreeNode left : leftList) {
                for(TreeNode right : rightList) {
                    TreeNode cur = new TreeNode(i);
                    cur.left = left;
                    cur.right = right;
                    rootList.add(cur);
                }
            }
        }
        return rootList;
    }

}

Python解法

​